Magnetometry and Precise Measurements of Atomic g Factor Ratios

We study the evolution of a spatially periodic superposition of magnetic sublevels of the ground state of Rb vapor in the presence of static magnetic fields. Two traveling wave pulses with orthogonal polarizations detuned from the excited state are applied at an angle of ~10 mrad to create a superposition of magnetic sublevels of the same hyperfine ground state. Magnetic sublevels differing by either Δm = 1 or Δm = 2 are coupled by the laser fields. The spatially periodic superposition dephases due to the velocity distribution of the sample. The dephasing can be detected by applying a traveling wave read out pulse along one of the excitation directions, and detecting the coherently scattered light along the other excitation direction. This coherent transient response is called magnetic grating free induction decay (MGFID). In the absence of magnetic fields, the temperature of a laser cooled sample inferred using the MGFID is in agreement with the temperature obtained by imaging the ballistic expansion of the sample. We have developed a theoretical description of the evolution of the MGFID in arbitrary static magnetic fields. The formulation describes the effect of the magnetic field as a time dependent rotation of the atomic system about the quantization axis using a rotation matrix approach. The predictions for the functional form of Larmor oscillations in the MGFID based on this approach are in excellent agreement with data from both room temperature vapor and laser cooled atoms. We are currently exploiting the properties of the MGFID for a precise determination of the ratio of atomic g factors using ⁸⁵Rb and ⁸⁷Rb. We have also used a rate equation approach to numerically simulate properties of the magnetic grating echo (MGE) in magnetic fields. The MGE can be observed by applying two sets of excitation pulses separated by t = T. The second excitation pulse cancels the effect of Doppler dephasing in the sample so that an echo is observed at t = 2T. In the presence of magnetic fields, experiments show that the MGE signal envelope develops Larmor oscillations. The MGE amplitude at t = 2T exhibits oscillations that depend on the Rabi frequencies of the excitation pulses and the magnetic field. These observations are consistent with simulations. Our results suggest that the MGE can be used to achieve a significantly improved measurement of the atomic g factor ratio.

Key Papers

Accurate determination of an alkali-vapour–inert-gas diffusion coefficient using coherent transient emission from a density grating, A. Pouliot, G. Carlse, T. Vacheresse, and A. Kumarakrishnan, SPIE Conference Proceedings 12016, 120160Q (2022)

Accurate determination of an alkali-vapour–inert-gas diffusion coefficient using coherent transient emission from a density grating, A. Pouliot, G. Carlse, H. C. Beica, T. Vacheresse, and A. Kumarakrishnan (York University), U. Shim, S. B. Cahn, A. Turlapov, and T. Sleator (New York University), Physical Review A 103, 023112 (2021)

Investigations of optical pumping for magnetometry using an auto-locking laser system, A. Pouliot, H. C. Beica, A. Carew, A. Vorozcovs, G. Carlse, B. Barrett, A. Kumarakrishnan, Proc. SPIE 10637, Laser Technology for Defense and Security XIV, 106370A (2018)

Prospects for Precise Measurements with Echo Atom Interferometry, B. Barrett, A. Carew, H. Beica, A. Vorozcovs, A. Pouliot, and A. Kumarakrishnan, Atoms, 4, 19 (2016)

A Precise Determination of Atomic g-factor Ratios from a Dual Isotope Magneto-Optical Trap, I. Chan, B. Barrett, and A. Kumarakrishnan,  Physical Review A 84, 032509 (2011)

Properties of Magnetic Sublevel Coherences for Precision Measurements, I. Chan, A. Andreyuk, S. Beattie, B. Barrett, C. Mok, M. Weel, and A. Kumarakrishnan, Physical Review A 78, 033418 (2008).

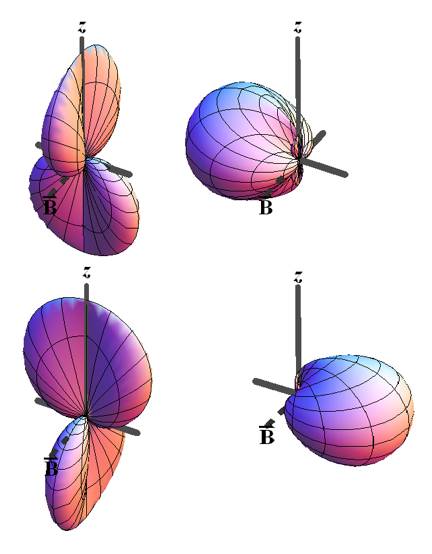Representation of evolution of coherences with J = 3.

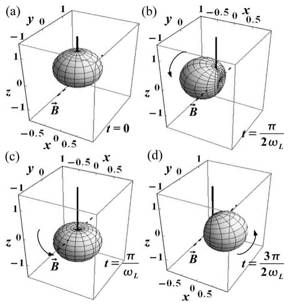
We consider the situation in which the quantization axis is along z (solid black line) and the magnetic field is along y (dotted line) for an atomic system with J = 1/2 .

(a) Surface ρ_1/2,1/2 (θ, φ, t) for t = 0.

(b) ρ_1/2,1/2 (θ, φ, t) for t = 1/4T_L

(c) ρ_1/2,1/2 (θ, φ, t) for t = 1/2T_L

(d) ρ_1/2,1/2 (θ, φ, t) for t = 3/4T_L .

Here, T_L = 2π/ω_L. The surface rotates around the direction of the magnetic field with frequency ω_L as a function of time.

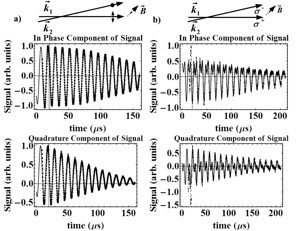Evolution of the in phase and quadrature parts of the MGFID in a sample of cold atoms. a) The excitation pulses have orthogonal linear polarizations and the magnetic field is directed at an angle of π/4 with respect to the polarization of k₁. b) The excitation pulses have opposite circular polarizations with the direction of the magnetic field at an angle of π/4 to the direction of k₁. In both cases the excitation pulses widths were 2 μs, and the detuning was 40 MHz. The data are shown as dots and the solid lines are fits based on theory.

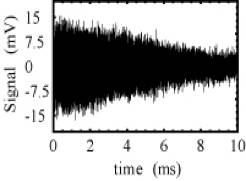
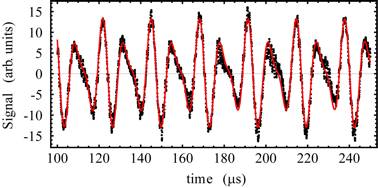
(a) Ground-state coherence signal from the dual isotope MOT. (b) Close up of the data displayed in (a) showing multiple-frequency components in the signal. Only one eighth of the points are displayed so that the fit (red line) and the data (black dots) can be distinguished. From a single shot, the ratio of effective atomic g factors is typically determined to a precision of∼1.5 ppm. (c) Seventy-five data sets acquired in ∼3 minutes. The error bars represent the fit uncertainties. The mean value is r =1.4988871and the (1σ) standard deviation of the mean is 1.0 x 10^-6 (0.69 ppm).