Precision Measurements of Atomic Recoil Frequency

The experiment involves a direct and precise measurement of the energy imparted to atoms by laser fields. A brief standing wave pulse of light is used to diffract atomic deBroglie waves. During the interaction with the light field, atoms absorb momenta in quantized units by absorption and stimulated emission of photons and return to the same internal state. The quantized units of momenta are 2nħk where n is an integer, ħ is h/2pi and k=2π/λ is the wave vector of light. Thus each atom evolves into a superposition of momentum states following laser interaction.

The atomic wave function is modulated at the atomic recoil frequency ω_r = ħbΔk²/2m (Δk is the momentum transferred by the laser field and m is the atomic mass) and the goal of the experiment is to measure the recoil energy ħω_r from a precise determination of the recoil period T_r = π/ω_r (~ 32 micro sec). ω_r can be related to h/m and measurement of h/m can be used to determine the atomic fine structure constant alpha much more precisely than a separate determinations of h or m. A measurement of alpha is of interest because it is a fundamental constant that governs the strength of light matter interactions and atomic structure.

Since the standing wave light potential is spatially modulated with a period λ/2, and the traveling wave components of this field are detuned far above the atomic resonance in a dilute gas (in this case, laser cooled Rb), atoms experience a channeling force toward the nodes of the potential. As a result, a density grating or one-dimensional optical lattice is formed in the sample. This is a transient effect that can be observed on a time scale of the order of the coherence time of the de-Broglie waves (a few μs). The relatively short coherence time is much smaller than the period of recoil modulation in the wave function (T_r). The coherence time can be increased by cooling the atomic sample well below the typical operating temperature of 50μK, which is the equilibrium temperature of atoms in the laser cooled sample. However, cooling the sample can increase the atomic density and produce density dependent systematic shifts in the recoil period. Consequently, we utilize a second standing wave pulse and the echo effect to observe the recoil modulation.

The second standing wave pulse applied at t = T interacts with the momentum states of each atom after they have drifted apart over macroscopic distances (much larger than the deBroglie wavelength). The interaction with the second pulse recombines the momentum states at t = 2T in a manner reminiscent of a photon echo. The interference of momentum states separated by 2ħk in the vicinity of t = 2T is associated with the formation of a density grating of period λ/2. The grating contrast can be detected by coherently backscattering a traveling wave from the cold sample. The intensity of backscattered light (known as a grating echo) exhibits a periodic modulation at ω_r as a function of T. The recoil period T_r can be measured with high by recording data over a large time interval and fitting the periodic function.

Since the atomic state internal state is a long lived ground state, the time scale of the experiment should be limited only by the transit time for cold atoms through the region of interaction. We have developed several techniques for measuring ω_r with high precision in both the time domain and the frequency domain. We are presently interested in further improving the time scale in an atomic fountain.

Key Papers

Prospects for Precise Measurements with Echo Atom Interferometry, B. Barrett, A. Carew, H. Beica, A. Vorozcovs, A. Pouliot, and A. Kumarakrishnan, Atoms, 4, 19 (2016)

Measuring the atomic recoil frequency using a modified grating-echo atom interferometer, B. Barrett, A. Carew, S. Beattie, and A. Kumarakrishnan, Physical Review A 87, 033626 (2013)

Atom interferometric techniques for measuring uniform magnetic field gradients and gravitational acceleration, B. Barrett, I. Chan, and A. Kumarakrishnan, Physical Review A, 84, 063623 (2011)

Time Domain Interferometry With Laser Cooled Atoms, B. Barrett, I. Chan, C. Mok, A. Carew, I. Yavin, (McMaster U.), A. Kumarakrishnan (York University), S, B. Cahn (Yale U.) and T.Sleator (NYU), Advances in Atomic, Molecular and Optical Physics Volume 60 Chapter 3, Elsevier (2011) (Edited by E. Arimondo, P.R. Berman and C.C. Lin)

Numerical Simulation of a Multilevel Atom Interferometer, B. Barrett, I. Yavin (NYU), S. Beattie, and A. Kumarakrishnan, Physical Review A 82, 023625 (2010).

Atom-Interferometric Studies of Light Scattering, S. Beattie, B. Barrett, I. Chan, C. Mok, I. Yavin (Princeton University), and A. Kumarakrishnan, Physical Review A (2009).

Technique for Measuring Atomic Recoil Frequency Using Coherence Functions, S. Beattie, B. Barrett, I. Chan, C. Mok, I. Yavin (Princeton University), and A. Kumarakrishnan, Physical Review A 79, 021605 (R) (2009).

Influence of Spontaneous Emission on a Single-State Atom Interferometer, S. Beattie, B. Barrett, M. Weel, I. Chan, C. Mok, S.B. Cahn (Yale), and A. Kumarakrishnan, Physical Review A 77, 013610 (2008).

Effect of a Magnetic Field Gradient and Gravitational Acceleration on a Time-Domain Grating-Echo Interferometer, M. Weel, I. Chan, S. Beattie, A. Kumarakrishnan (York University), D. Gosset (UBC), and I. Yavin (Harvard U), Physical Review A 73, 063624 (2006).

Measurements of Temperature Scaling Laws In an Optically Dense Magneto-Optical Trap, A. Vorozcovs, M. Weel, S. Beattie, S. Cauchi, and A. Kumarakrishnan, Journal of the Optical Society of America B 22, 943 (2005).

Observation of Ground State Ramsey Fringes, M. Weel, and A. Kumarakrishnan, Physical Review A 67, 061602(R), (2003).

A Calculation of the Time-of-Flight Distribution of Trapped Atoms, I. Yavin, M. Weel, A. Andreyuk, and A. Kumarakrishnan, American Journal of Physics 70, 149 (2002).

a) Experimental setup using a single, retro-reflected beam.

b) Experimental setup using two separate, counter-propagating beams.

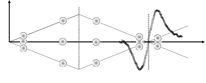
Billiard ball representation of the momentum states associated with the interferometer. Only three possible trajectories (0, ±ħq) due to the first excitation pulse are shown. A subset of higher-order processes (±2ħq, ±3ħq, etc.) can be rephased at t = 2T, but only trajectories differing by ħq contribute to the signal at t = 2T. The echo envelope is also shown in the vicinity of t = 2T and its temporal width is inversely proportional to the velocity distribution. Here, the time interval between extrema is ~2 μs, T~1–30 ms, and T_recoil = π/ω_q ~32 μs.

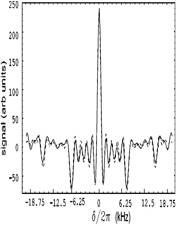
A typical recoil measurement with Δ = 50 MHz. The measurement is carried out by fitting the data to theory and consists of one recoil period recorded at T ~ 900 μs (a) and a second recoil period recorded at T ~ 9000μs (b). The fit gives ωq = 97 008.5(4) s^-1.

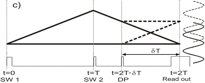
 New method of measuring atomic recoil, showing effect of a decoherence pulse (DP) on the atom interferometer (AI). Two interfering momentum states (solid black lines) are perturbed by a DP applied at t = 2T − δT. The DP can affect both arms of the interferometer resulting in interference between displaced trajectories (dashed lines) that is phase shifted with respect to the original interference pattern. Constructive interference is observed if δT = nT_r where n is an integer.

Observed Ramsey fringe pattern; solid line is data; dashed line is fit which yields ω_r = 97.0 × 10³ s^-1 and θ₂ = 1.8.

a) Measurement of ω_r using a single sw DP with duration τ = 150 ns. The fit gives ω_r = 97.0032 ± 0.00016 kHz.

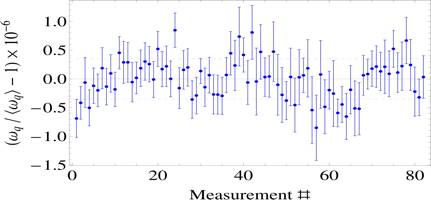
Recoil frequency measurement precise to 220 ppb using a time scale of 90 ms and a fringe width of ~2 ms. The data was acquired in 10 minutes. Analysis of 82 similar measurements recorded under the same conditions over 14 hours of interrogation time shows an average precision of 380 ppb. The resulting uncorrected value of the recoil frequency was measured with a precision of 37 pbb (standard deviation of the mean).

AI signal lifetime for two-pulse and various three-pulse configurations in a glass cell with a sample temperature of T ∼ 20 mK. The horizontal axis is the time of the read-out pulse, T_RO, relative to the time of trap turn-off, T₀, which signifies the start of the experiment. The three-pulse AI is less sensitive to B gradients and vibrations than the two-pulse AI. Decoherence due to these effects is limited by adjusting the pulse spacing T₂₁, which controls the separation between wave packets so that the measurement time scale is comparable to the transit time.