Numerical Simulations of Matter Wave Interference

Monte Carlo wave function (MCWF) simulations can be used to understand many interesting signatures of a single state atom interferometer. Examples include the characteristics of the echo signal from the interferometer, the relative population of momentum states, the influence of spontaneous emission on the echo signal and the behaviour of the interferometer in the Bragg regime. The MCWF method is a well-known approach for solving dissipation problems in quantum optics. The method is equivalent to a master equation approach, but the random nature of quantum jumps is simulated more directly using a Monte Carlo treatment.

Key Papers

Numerical Simulation of a Multilevel Atom Interferometer, B. Barrett, I. Yavin (NYU), S. Beattie, and A. Kumarakrishnan, Physical Review A 82, 023625 (2010).

(a) Evolution of the position space probability density as a function of time after the first excitation pulse for a T ~ 10 nK sample. The pulse parameters are Ω₀ = 1 Γ_n, Δ =10 Γ_n and δt₁ = 4 τ_n.

(b) Evolution of 2k_L Fourier component of density distribution shown in (a), which represents the experimental signal. A fit to the signal, shown in gray, gives a recoil frequency ω_q = 2π × 15.430(1) kHz and temperature T ~ 7 nK, which is consistent with the input temperature.

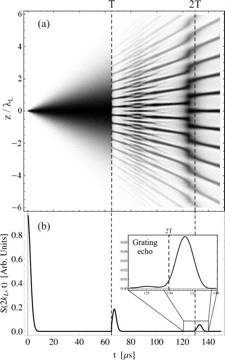(a) Evolution of the position space probability density after two sw excitation pulses for a T = 10 μK sample. The pulse parameters are Ω₀ = 2 Γ_n, Δ = 4 Γ_n, δt₁ = δt₂ = 4 τ_n and T = 2 τ_q = 64.77 μs.

(b) Evolution of 2k_L Fourier component of density distribution shown in (a). The signal decays exponentially after each excitation pulse due to Doppler dephasing on a timescale consistent with t_coh ~ 4 μs. In the vicinity of t = 2T, interference between momentum states creates a modulation in the density distribution and the grating echo is formed.

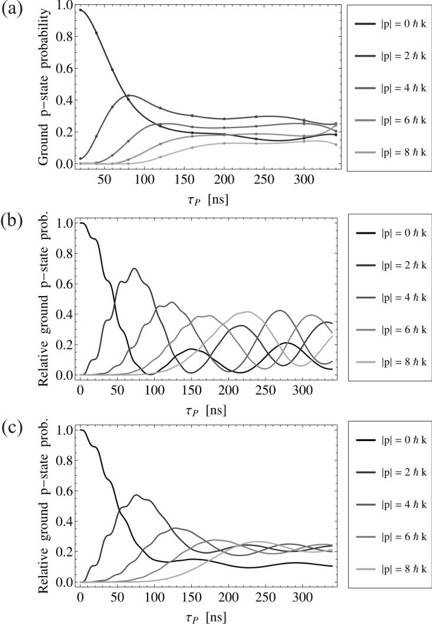
Probabilities of momentum states associated with the ground state versus τDP; probabilities extracted from fits using g_f (δT), Δ = 39 MHz and Ω ~ 18 MHz. The points are joined using a 5^th order interpolation function.

b) MCWF simulations neglecting the effects of spontaneous emission and spatial profile showing probabilities versus τDP; Δ = 39 MHz and Ω = 18 MHz.

c) MCWF simulations including the effects of spontanoues emission and spatial profile for the same conditions as in b).